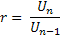BARISAN DAN DERET

on

Barisan dan Deret

A.      BARISAN DAN BILANGAN

      Barisan bilangan merupakan rangkaian bilangan yang teratur, misalkan :
·         1, 2, 3, 4, 5,…
·         2, 4, 6, 8,…
Secara umum barisan tersebut disebut Suku, sehingga
·         U1 : suku pertama
·         U2 : suku ke dua
·         U3 : suku ke 3, dst
Misalkan terdapat barisan : 1, 3, 5, 7,…
·         Suku ke 2 U2 = 3 = 2(2) – 1
·         Suku ke 5 U5 = 9 = 2(5) – 1

Un = 2n - 1

         Jumlah n suku yang pertama suatu deret dinyatakan dengan :

Sn = U1+U2+U3+...Un

B.      BARISAN DAN DERET ARITMATIKA

1.       BARISAN ARITMATIKA

Barisan aritmatika berlaku jika  : U2 – U1 = U3 – U2 = U5 – U4 = dst, sehingga Beda dari barisan aritmatika dinyatakan dengan :

b = Un–Un-1

Contoh :
Tentukan beda dari barisan : 5, 10, 15, …
B = U2 – U1 = 10 – 5 = 5

2.       SUKU KE n BARISAN ARITMATIKA

Un=a+(n-1)b

Un : suku ke n
a : suku pertama
b : beda

Contoh :
Tentukan suku ke 100 dari barisan : 5, 8, 11, …
Un = a + (n – 1)b = 5 + (100 -1)3 = 302, jadi
U100 = 302

3.       JUMLAN n SUKU DERET ARITMATIKA

Sn = ( a + Un)
atau
Sn = (2a + (n – 1)b)

Contoh :
Hitung jumlah deret aritmatika  8 + 11 + 14 + 17 + … sampai 40 suku
a = 8, b = 3, n = 40
S40 = (2.8 + (40 – 1)3)
S40 = 3.860
C.      BARISAN DAN DERET GEOMETRI

Disebut barisan Geometri jika belaku :
 =  =  = …
Bilangan konstan / beda dinyatakan dengan


Contoh :
Tentukan Rasio dari barisan 3, 9 , 27, 81, …

1.       SUKU KE n BARISAN GEOMETRI

Un = a.rn-1

Contoh :
Tentukan suku ke 10 barisan 1, 2, 4, 6, 8,…
Un = a.rn-1 = 1.210-1 = 512

Diketahui suku ke 3 barisan geometri adalah 36 dan suku ke 5 adalah 81, tentukan suku pertama dan rasionya…
U5 = a.r4 = 81
U3 = a.r2 = 36 :
           r2 =   … r =
a.r2 = 36 … a = 16

2.       JUMLAH n SUKU DERET GEOMETRI

         a(1 - rⁿ)
Sn = ─────, jika r < 1
          1 - r

         a(rⁿ - 1)
Sn = ─────, jika r > 1
          (r - 1)

Contoh :
Hitung jumlah 10 suku dari deret 3 + 9 + 27 +
a = 3
r = U2/U1 = 9/3 = 3
n = 10
         a(r^n - 1)      3(3^10 - 1)     
Sn = ────── = ────── = 88572
           (r - 1)             3 - 1
3.       DERET GEOMETRI TURUN TAK HINGGA

Berlaku pada rasio -1 < r < 1 dan disebut juga sebagai  deret Konvergen
           a
S = ────
        1 - r

Contoh :
Tentukan jumlah suku-suku deret geometri tak hingga dari 1 + 1/3 + 1/9 + 1/27...
a = 1
r = (1/3) / 1 = 1/3
              1               1
S  = ────── = ─── = 3/2
         1 - (1/3)        2/3